Some note of Big-O Notation
Some Algorithm basic that Data Scientist easy to skip.
- It begins with a story
- Introducing the Big-O Notation
- An Anagram Example
- Some Exercise Again?
- Exercise Solution:
It begins with a story
I always recall that when I was kid, my math teacher love to ask a question:
- Who can tell me the answer of adding 1 to 100?
Some student started to calculate: $1+2+3+4+5+6+7+......$.
The one who always get No.1 in class tell the answer in a very short time: It's $5050$
Teacher ask: "How you do that?"
He said: "Well, $1+100$ is $101$, and $2+99$ is $101$, there's total $50$ of $101$, so that answer is $50 \times 101$, which is $5050$.
The smart boy definitely not me, I am the one who record this story, but it do inspire me the extended question: What if we are not adding 1 to 100, but adding 1 to n?
Let's solve this question by writing a function to sum from 1 to $n$. That's simple:
Python Solution 1
def summation(n):
result = 0
for i in range(1, n+1):
result += i
return result
array = [1, 2, 3, 4, 5]
summation(5) == sum(array) #expected True
Python Solution 2
def summation(n):
return n * (n + 1) // 2
array = [1, 2, 3, 4, 5]
summation(5) == sum(array) #expected True
Can you tell me which algorithm is better? and Why?
Some will say: "I think the Solution 1 is better, because the Zen of Python said Readability Count, the Solution 1 is very easy to understand at the first glance, you know what it's doing at the very begnning. "
Some will say: "I think the Solution 2 is better, because it always one step to get the answer."
Well, that's close, let's do the step by step analysis to compare this two solution:
Solution 1:
Let's say the $n$ is $5$:
- Step 1: initialized
result = 0 - Step 2: Start the loop from
i = 1, thenresult = 1 + 0 = 1 - Step 2: In the Loop: now
i = 2, execute:result = 1 + 2 = 3 - Step 3: In the Loop: now
i = 3, execute:result = 3 + 3 = 6 - Step 4: In the Loop: now
i = 4, execute:result = 6 + 4 = 10 - Step 5: In the Loop: now
i = 5, execute:result = 10 + 5 = 15 - Step 6: return the
resultvalue.
Solution 2:
Let's say the $n$ is $5$:
- Step 1: return the value: $\frac{5 \times (5 + 1)}{2} = 15$
Ok, in the first solution, the Steps will grows when the $n$ grows, let's say the $n$ is millions, then the function need to execuate millions time to get the answer. In contrast, no matter how big is the $n$, in the second solution, there will be always one time execuation to get the answers, so no matter in a slower computer, or a super fast computer, Solution 2 will be always faster than the Solution 1
Above analysis it just qualitative, what science need is precise, so what's the quantitative analysis for it to precisely identify and analyse the algorithm?
Introducing the Big-O Notation
When trying to characterize an algorithm’s efficiency in terms of execution time, independent of any particular program or computer, it is important to quantify the number of operations or steps that the algorithm will require. If each of these steps is considered to be a basic unit of computation, then the execution time for an algorithm can be expressed as the number of steps required to solve the problem. Deciding on an appropriate basic unit of computation can be a complicated problem and will depend on how the algorithm is implemented.
In the summation functions given above, it makes sense to use the number of terms in the summation to denote the size of the problem. We can then say that the sum of the first 100,000 integers is a bigger instance of the summation problem than the sum of the first 1,000. Because of this, it might seem reasonable that the time required to solve the larger case would be greater than for the smaller case. Our goal then is to show how the algorithm’s execution time changes with respect to the size of the problem.
Computer scientists prefer to take this analysis technique one step further. It turns out that the exact number of operations is not as important as determining the most dominant part of the $T(n)$ function. In other words, as the problem gets larger, some portion of the $T(n)$ function tends to overpower the rest. This dominant term is what, in the end, is used for comparison. The Order of Magnitude function describes the part of $T(n)$ that increases the fastest as the value of $n$ increases. Order of magnitude is often called Big-O Notation(for Order) and written as $O(f(n))$. It provides a useful approximation to the actual number of steps in the computation. The function $f(n)$ rovides a simple representation of the dominant part of the original $T(n)$.
Common Functions for Big-O:
$n$ --> The size of the input
- Constant runtime(Time Complexity): $O(1)$
- Logarithmic runtime(Time Complexity): $O(\log (n))$
- Linear runtime(Time Complexity): $O(n)$
- LinearLogarithmic runtime(Time Complexity): $O(n\log (n))$
- Quadric runtime(Time Complexity): $O(n^2)$
- Cubic runtime(Time Complexity): $O(n^3)$
- Exponential runtime(Time Complexity): $O(b^n), b > 1$
- Factorial runtime(Time Complexity): $O(n!)$
If we plot the graph of each run time:
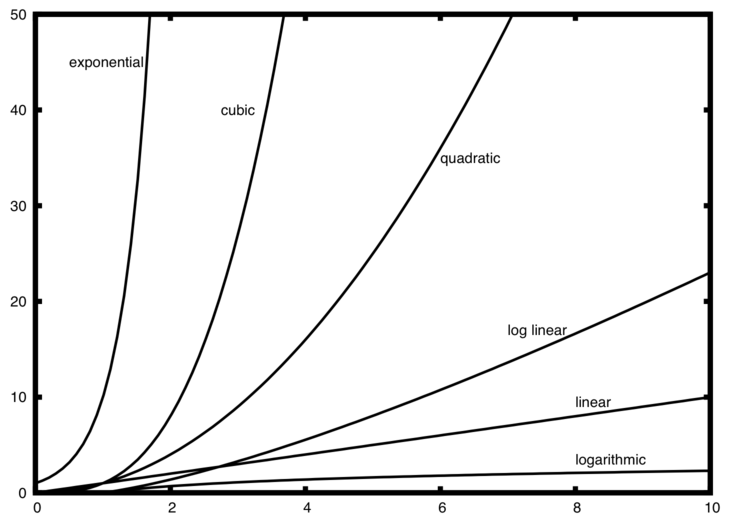
So if we visit back our begins story. What do you think the Time Complexity of Solution 1 and Solution 2? Comment below.
Big-O Notation Rules:
Rule 1: Different Steps get added
Example
def doSomething():
doStep(a) #O(a)
doStep(b) #O(b)
return
So for the above example, the Time Complexity should be: $O(a+b)$
Rule 2: Drop Constants
Example
One
def minMax(array):
minimum, maximum = None, None
for i in array:
minimum = min(i, minimum)
for i in array:
maximum = max(i, maximum)
return minimun, maximum
Two
def minMax(array):
minimum, maximum = None, None
for i in array:
minimum = min(i, minimum)
maximum = max(i, maximum)
return minimum, maximum
The above TWO functions do the same thing, return the min and max value from an array, but the One is first find the min, and then find the max, so the actual steps is 2n, while the Two is finding the min, max concurrently, so the actual steps is n.
You may say the One time complexity is O(2n) and Two time complexity is O(n), the actual answer is both of them time complexity is O(n), because when the n approach to inf, the constant 2 will be less significant till can be ignored, so this is the Rule 2: Drop the constant
Rule 3: Different Inputs --> Different Variables
Example
def intersectionSize(arrayA, arrayB):
count = 0
for a in arrayA:
for b in arrayB:
if a == b:
count += 1
return count
Well, this function have loop in the loop, we can easily identify it as $O(n^2)$ of time complexity, but actually is False, let's ask a simple question, what is the n means? well, we may say n is the input size of the array, ok, then which array? arrayA or arrayB? since this is different variables, and the n repersent different variable input size, here we should describe the time complexity as:
- $O(a \times b)$
Rule 4: Drop the non-dominant terms
Example
def IdontKnowWhatIamDoing(array:list):
maximun = None
# O(n) Time complexity
for i in array:
maximun = max(a, maximum)
print(maximum)
# O(n^2) Time complexity
for a in array:
for b in array:
print(a, b)
We can see from above function IdontKnowWhatIamDoing, the 1st part's time complexity is $O(n)$, and the 2nd parts' time complexity is $O(n^2)$, does it mean the total time complexity is $O(n + n^2)$?
Well, let's do some simulation:
- if
n = 1, there's $O(1 + 1^2 = 2)$ - if
n = 2, there's $O(2 + 2^2 = 5)$ - if
n = 10, there's $O(10 + 10^2 = 110)$ - if
n = 10,000, there's $O(10,000 + 10,000^2 = ???)$ - if
n = 100,000, there's $O(100,000 + 100,000^2)$
What pattern do you found? when the n grows, the $n^2$ have more dominance, and the $n$ part become less significant, in the Big-O Notation, we are not doing the details computation, Big-O notation is the unified way to describe an algroithm's time complexity and space complexity(may discuss next post), so we just need to know the donimant term that impact the run time the most. so here we drop the non-dominant term, the time complexity is:
- $O(n^2)$
Some Exercises?
We have finished the Rules of Big-O Notation, how about a small exercises? it can be solved based on the info above:

An Anagram Example
What is Anagram?
We have a word table here:
| Word_1 | Word_2 |
|---|---|
| earth | heart |
| planet | platen |
| space | paces |
| star | rats |
| cosmic | comics |
| nebula | unable |
| lunar | ulnar |
| solar | orals |
| sunspots | unstops |
Can you find the pattern? Is there any relationship bewteen the word_1 and word_2?
In layman term, Anagram is those words, really meaningful word, have the identical letters with others meaningful word:
- Meaningful
- formed by same letter
Just like earth and heart.
So now we know what's Anagram, now write a short function to tell whether this two words is Anagram or not, the function should accept two string, and return a bool value of True or False to tell whether this two words is Anagram or not.
Solution 1: Checking Off
Our first solution to the anagram problem will check the lengths of the strings and then to see that each character in the first string actually occurs in the second. If it is possible to “checkoff” each character, then the two strings must be anagrams. Checking off a character will be accomplished by replacing it with the special Python value None However, since strings in Python are immutable, the first step in the process will be to convert the second string to a list. Each character from the first string can be checked against the characters in the list and if found, checked off by replacement.
def isAnagram(string1:str, string2:str) -> bool:
anagram = True
if len(string1) != len(string2):
anagram = False
stringList = list(string2)
position_1 = 0
while position_1 < len(string1) and anagram:
position_2 = 0
found = False
while position_2 < len(stringList) and not found:
if string1[position_1] == stringList[position_2]:
found = True
else:
position_2 += 1
if found:
stringList[position_2] = None
else:
anagram = False
position_1 += 1
return anagram
print(isAnagram('earth', 'heart')) # expected: True
print(isAnagram('abc', 'abcde')) # expected: False
To analyze this algorithm, we need to note that each of the n characters in string1 will cause an iteration through up to n characters in the list from string2. Each of the n position in the list will be visited once to match a character from string1. The number of visits then becomes the sum of the integers from 1 to n. We stated earlier that this can be written as:
$$\sum_{i=1}^{n}i = \frac{n(n+1)}{2}$$ $$= \frac{1}{2}n^2 + \frac{1}{2}n$$
As n gets large, the $n^2$ term will dominate the n term and $\frac{1}{2}$ can be ignored. Therefore, this solution time complexity is:
- $O(n^2)$
Solution 2: Sort and Compare
I am not sure did you notice there's one more pattern of Anagram, is actually both words will have the same length, well, we can come up an other solution that convert the string into list, then use Python's bulit function sorted() to sort this two list, and return the compare boolean value:
This actually a Pythoinc Solution, which may not suitable to other languages
del isAnagram #delete function for clear
def isAnagram(string1:str, string2:str) -> bool:
return sorted(string1) == sorted(string2)
print(isAnagram('earth', 'heart')) # expected: True
print(isAnagram('abc', 'abcde')) # expected: False
print(isAnagram('cosmic', 'comics')) # expected: True
We may come up with similar solution that not so Pythonic, being more language neutral
del isAnagram # delete function for clear
def isAnagram(string1:str, string2:str) -> bool:
stringList1 = sorted(string1)
stringList2 = sorted(string2)
position = 0
matches = True
if len(stringList1) != len(stringList2):
return False
while position < len(stringList1) and matches:
if stringList1[position] == stringList2[position]:
position += 1
else:
matches = False
return matches
print(isAnagram('earth', 'heart')) # expected: True
print(isAnagram('abc', 'abcde')) # expected: False
print(isAnagram('cosmic', 'comics')) # expected: True
At first glance you may be tempted to think that this algorithm is $O(n)$, since there is no simple iteration to compare the $n$ characters after the sorting process. However, the two calls to Python sorted() method are not without their own cost. As we go deeper in Python, sorting is typically either $O(n^2)$ or $O(n \log n)$, so the sorting operations dominate the process. In the end, this algorithm will have the same order of magnitude as the previous solution, which is:
- $O(n^2)$
Solution 3: Count and Compare
The 4th Solution to the Anagram problem takes advantage of the fact that any two Anagrams will have the same numbers of characters, such as same number of a, same number of b, and so on. In order to decide whether two strings are Anagrams, we will first count the number of times for each characters. Since there are 26 possible characters, we can use a list of $26$ counters, one for each possible character, just like One-Hot encoding in Data Science.
Same as Solution 2, we have one Pythonic Solution, and one non Pythonic solution:
Pythonic Solution
from collections import Counter
del isAnagram # delete function for clear
def isAnagram(string1:str, string2:str) -> bool:
if len(string1) != len(string2):
return False
return Counter(string1) == Counter(string2)
print(isAnagram('earth', 'heart')) # expected: True
print(isAnagram('abc', 'abcde')) # expected: False
print(isAnagram('cosmic', 'comics')) # expected: True
Non Pythonic Solution
The key is we will one-hot encoding the string into a list of $26$ characters.
Example
string1 = 'apple'
# after one-hot encoding
[1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
According to the list, character a in index 0 appear 1 times, character e in index 4 appear 1 times.
We will convert two string into this list, and make a pointer, started from index 0 to compare the appearing times for each characters, if match, then we can say this two strings is Anagrams. So this Algorithm do not have sorting, the time complexity should be $O(n)$
del isAnagram # delete function for clear
def isAnagram(string1:str, string2:str) -> bool:
if len(string1) != len(string2):
return False
# construct empty one-hot encoding list
stringList1 = [0] * 26
stringList2 = [0] * 26
# iterate to contruct the one-hot encoding
for i in range(len(string1)):
position = ord(string1[i]) - ord('a')
stringList1[position] += 1
for i in range(len(string2)):
position = ord(string2[i]) - ord('a')
stringList2[position] += 1
pointer = 0
anagram = True
while pointer < 26 and anagram:
if stringList1[pointer] == stringList2[pointer]:
pointer += 1
else:
anagram = False
return anagram
print(isAnagram('earth', 'heart')) # expected: True
print(isAnagram('abc', 'abcde')) # expected: False
print(isAnagram('cosmic', 'comics')) # expected: True
Again, the solution has a number of iterations. However, unlike the first solution, none of them are nested. The first two iterations used to count the characters are both based on n. The third iteration, comparing the two lists of counts, always takes $26$ steps since there are $26$ possible characters in the strings. Adding it all up gives us $T(n) = 2n + 26$ steps, That is $O(n)$. We have found linear order of magnitude algorithm for solving this problem.
Some Exercise Again?
-
Given the following code fragment, what is its Big-O running time?
test = 0 for i in range(n): for j in range(n): test = test + i * j
-
Given the following code fragment, what is its Big-O running time?
test = 0 for i in range(n): test += 1 for j in range(n): test -= 1
-
Given the following code fragment, what is its Big-O running time?
i = n while i > 0: k = 2 + 2 i = i // 2
Exercise Solution:
Still reading? now solution time:
